2413 字
12 分钟
matlab图像绘制
2021-10-18
编程学习
matlab
/
数据绘图

图形绘制基本流程#

1.准备绘图数据

2.创建绘图窗口

3.调用绘图函数

4.设置样式与标记属性

5.设置坐标范围与网格属性

6.设置色表

7.设置光照效果

8.设置视角

9.给图形添加标注

10.到出或保存图形

基本流程详解#

准备绘图数据#

常见有函数、矩阵等

例：

y=sin(x)+2*cos(x);

创建图形窗口#

figure;

一般在脚本文件中不用写此句，调用绘图函数会自动创建

需要注意的是，在修改程序后下一次执行程序前注意执行 close all 否则默认在现有窗口中继续绘图

窗口命令#

image-20211023232258258

调用绘图函数#

二维#

image-20211023182414266

二维曲线#

plot() 二维曲线#

plot(X,Y,LineSpec)

设置线型、标记符号和颜色。

linespec默认值#

linespec非必需值，不填写默认实线，无标记

x = 0:pi/100:2*pi;
y = sin(x);
plot(x,y)

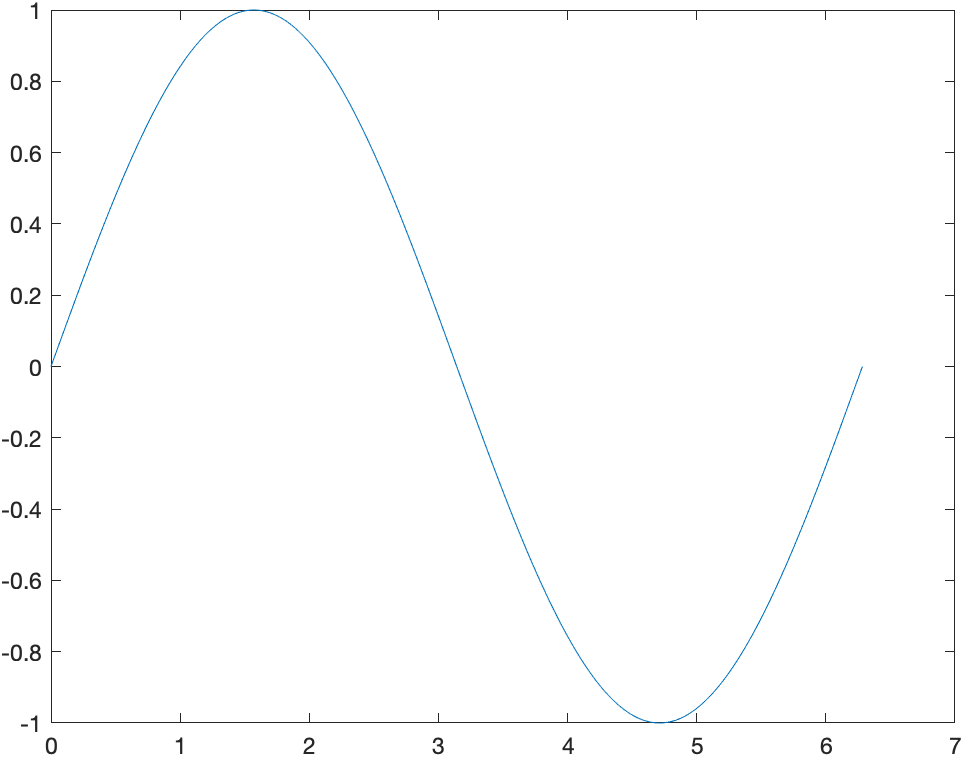
image-20211016221247668

设置linespec并绘制多个函数#

可一个函数在单个图中绘制多个

x = 0:pi/10:2*pi;
y1 = sin(x);
y2 = sin(x-0.25);
y3 = sin(x-0.5);

figure
plot(x,y1,'g',x,y2,'b--o',x,y3,'c*')

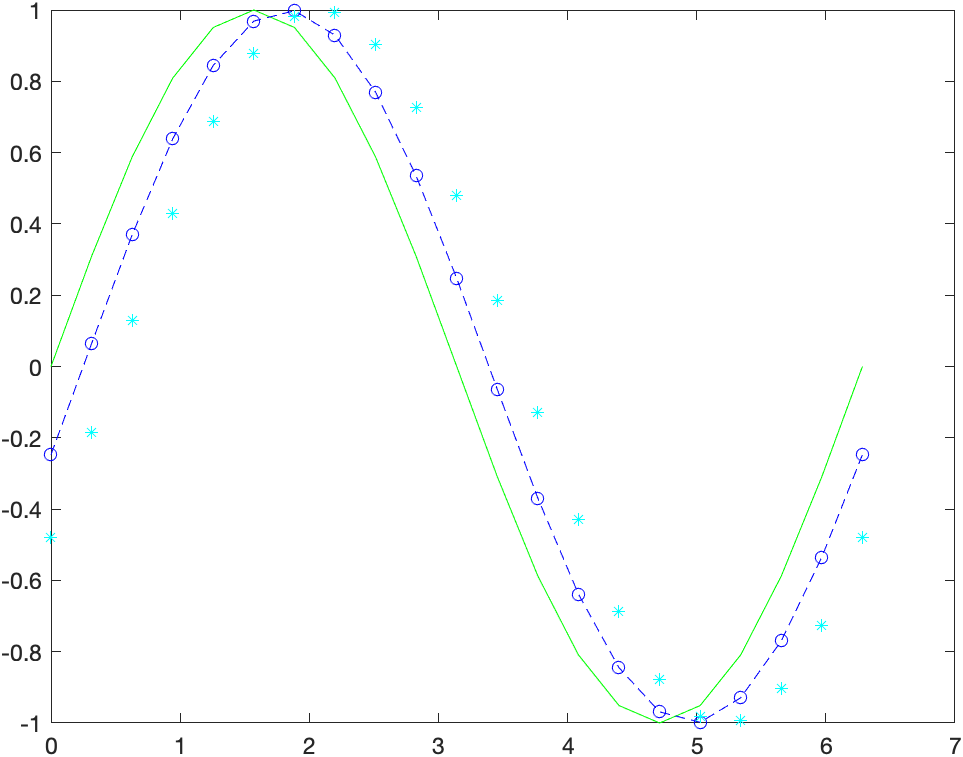
image-20211016221210047

创建矩阵线图#
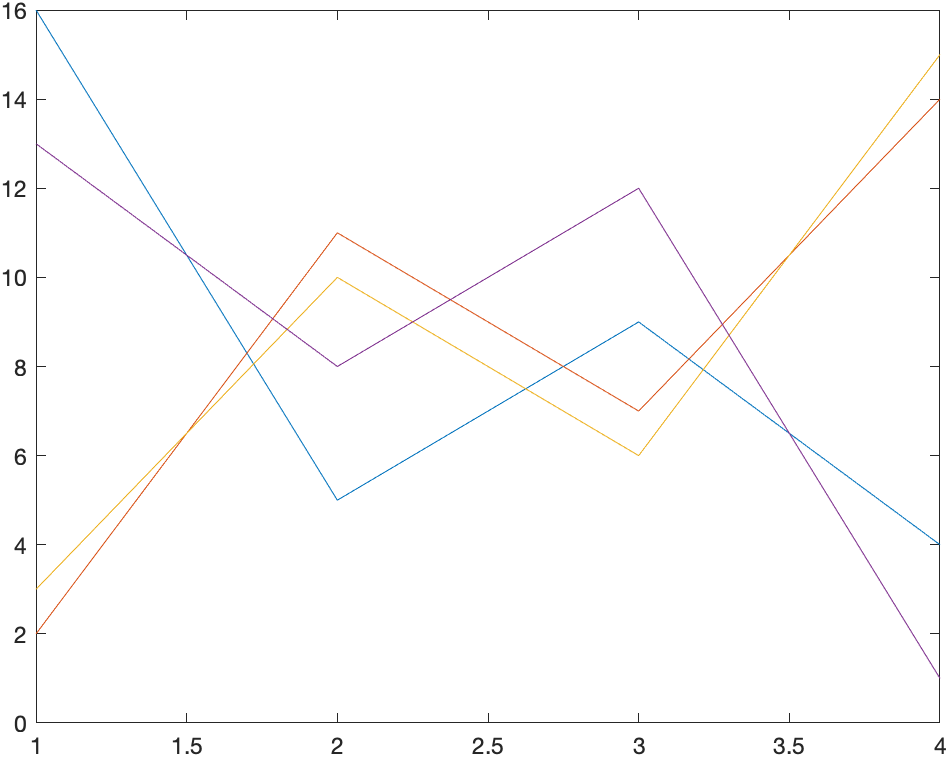
Y = magic(4)  %幻方矩阵
figure
plot(Y)

创建 Y 的二维线图。MATLAB将矩阵的每一列绘制为单独的线条。

image-20211016221653254

line() 二维曲线#

line(x,y,‘name’,‘value’）

截屏2021-10-17 上午12.16.33

image-20211017001822555

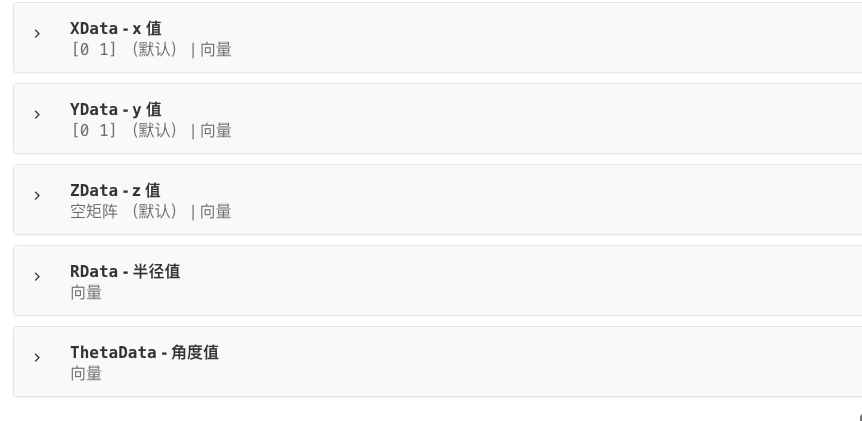
image-20211017001839183

image-20211017001745725

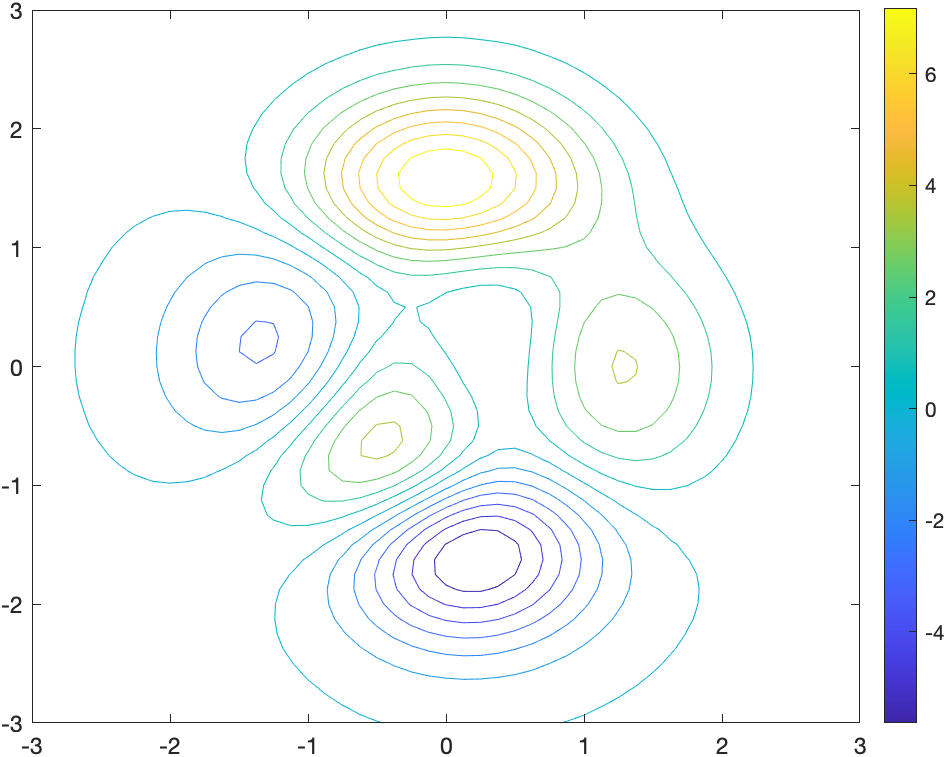
等高线图——平面#

contour()

把曲面的等高线投影在X-Y平面

close all 
[x,y,z]=peaks;
contour(x,y,z,15);
colorbar;

image-20211023235429266

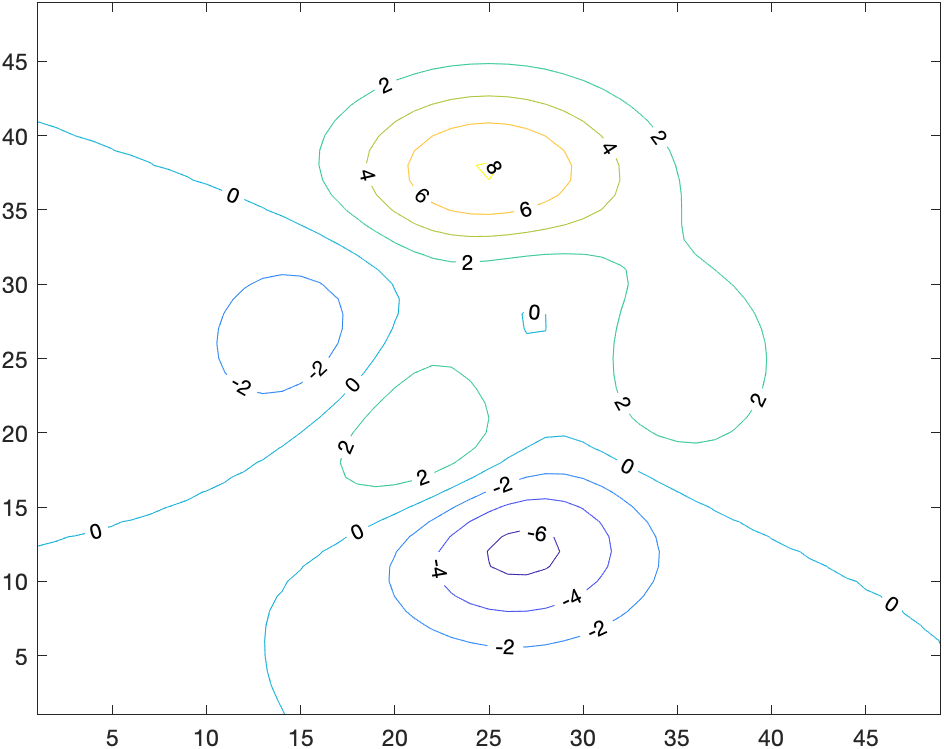
添加高度标签#

[c,h]=contour(…)

返回等高线矩阵c，和等高线对象的句柄h，c中 包含每个层级的顶点的 (x, y) 坐标。

[x,y,z]=peaks;
[c,h]=contour(z);
clabel(c,h);

image-20211023235555176

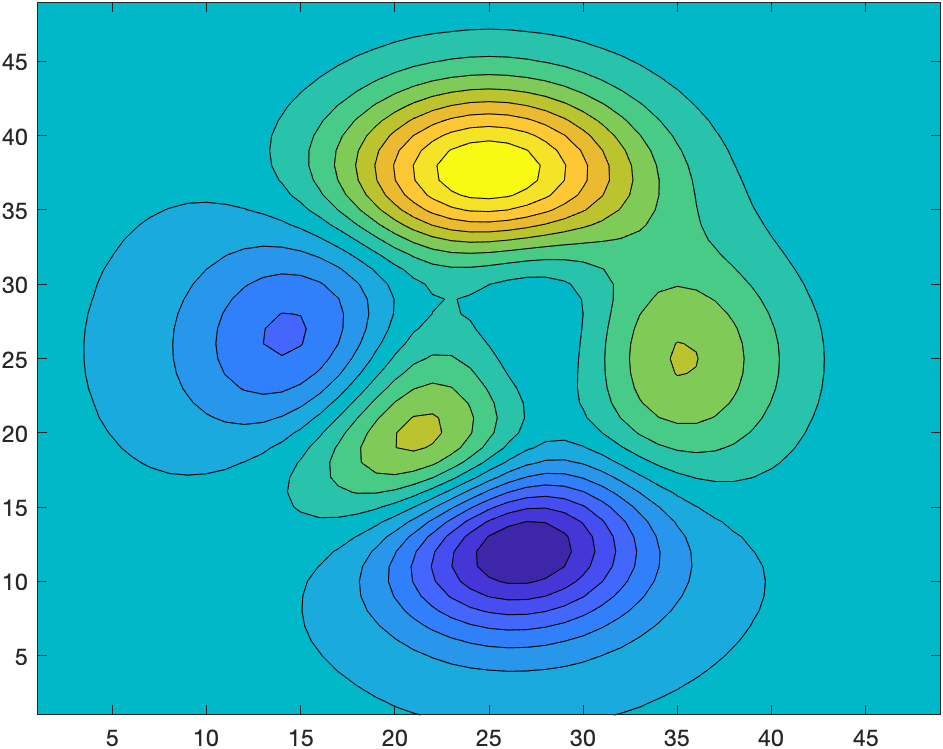
填充二维等高线图#

contourf()

[x,y,z]=peaks; 
contourf(z,15);

image-20211023235908328

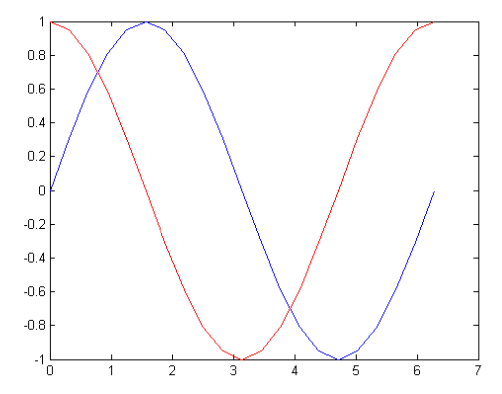
hold 多图绘制#

hold on  %开启叠加模式
hold off %关闭叠加模式

示例

x = 0:0.1*pi:2*pi;
y = sin(x);
plot(x,y);
% 设置为叠加绘图模式 hold on
z = cos(x);
% 绘制第二条曲线，颜色为红色 
plot(x,z, ‘r’);
% 关闭叠加模式
hold off

image-20211017003717150

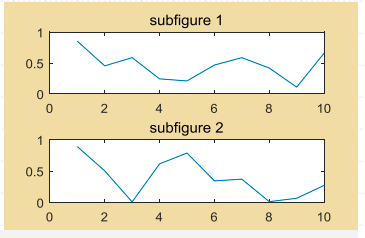
subplot()子图绘制#

subplot函数的一般语法形式为： subplot(m, n, p) 5.2.6 子图绘制 执行该语句，即可在当前绘图区中创建m×n个绘图子区， 并将第p个绘图子区选定为当前绘图区。

x = 1:1:10;
y = rand(1, 10); % 随机生成包含10个元素数组y
z = rand(1, 10); % 随机生成包含10个元素数组z
subplot(2, 1, 1); % 选择2行1列子图中第1个子图
plot(x, y);
title('subfigure 1');
subplot(2, 1, 2); % 选择2行1列子图中第2个子图
plot(x, z);
title('subfigure 2');

image-20211017004018274

特殊图形绘制#

绘制柱状图#

bar(x,y,‘style ’)

barh() 是bar()的横向

style#
’grouped’#

为 y 中的每一行显示一组。

如果 y 是一个 m×n 矩阵，bar 显示 m 组 n 个垂直条，其中，m 是 y 的行数，n 是列数。

如果 y 是长度为 n 的向量，bar 会显示由 n 个条形构成的一个条形组。bar 函数将所有向量当作列向量处理。

‘stacked’#

为 y 中的每一行显示一个条形。

如果 y 是一个 m×n 矩阵，bar 显示 m 个条形，其中每个条形高度是行中元素总和。每个条形标记有多种颜色。不同颜色分别对应不同的元素，显示每行元素占总和的相对量。

如果 y 是长度为 n 的向量，则 bar 会显示 n 个条形。bar 函数将所有向量当作列向量处理。

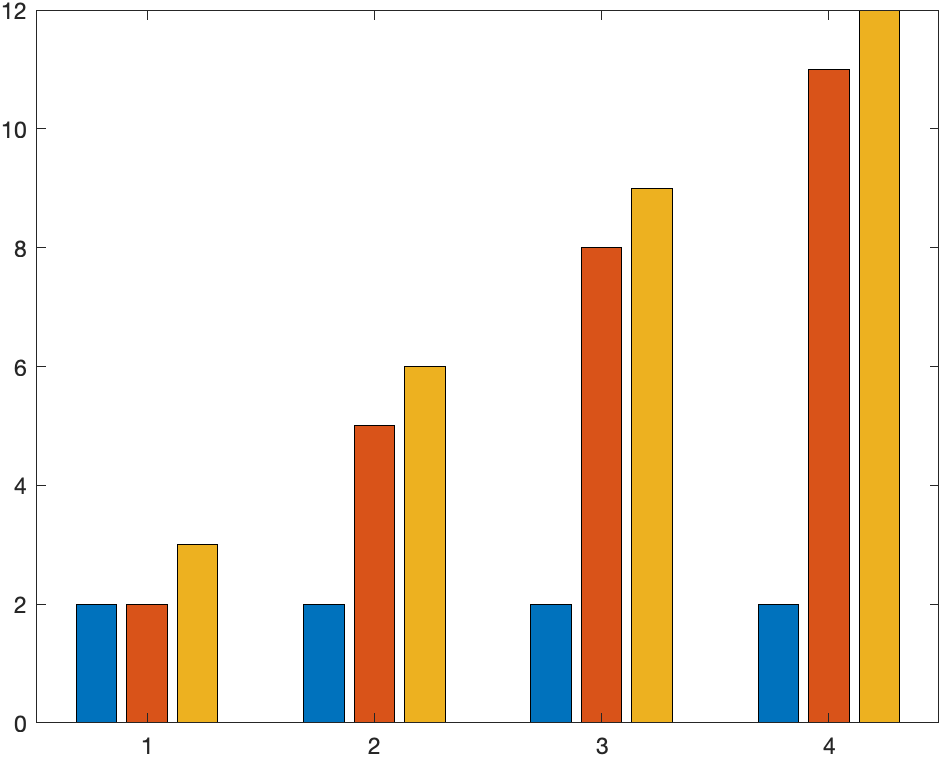
y = [2 2 3; 2 5 6; 2 8 9; 2 11 12];
bar(y)

image-20211022153711624

绘制面积图#

area(x,y)

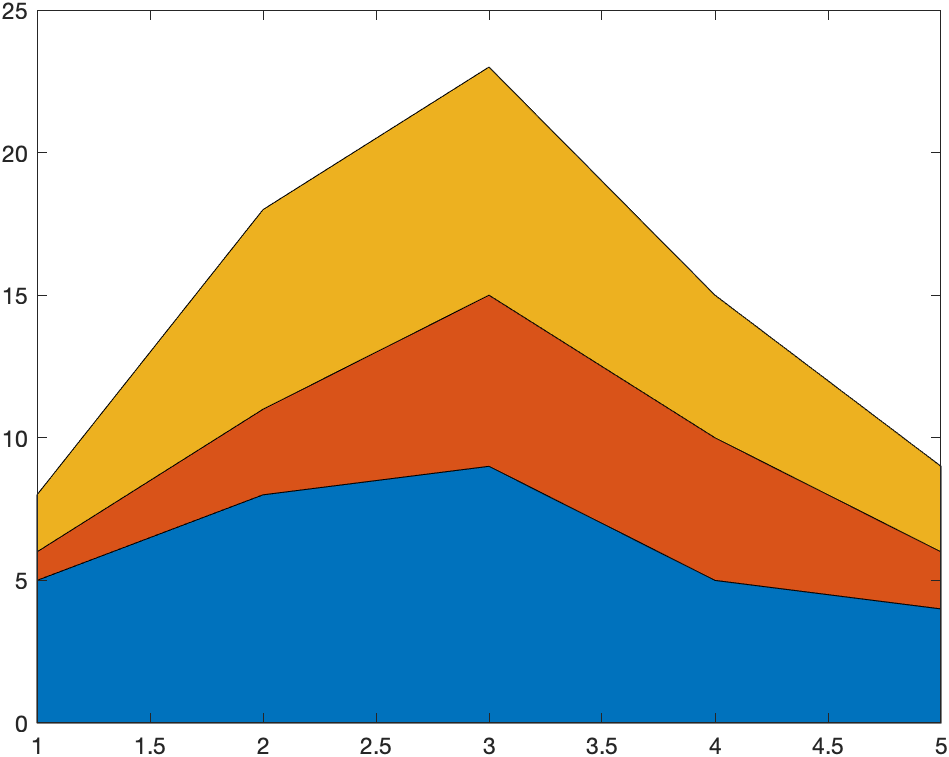
X = [1;2;3;4;5]; 
Y = [5 1 2;8 3 7; 9 6 8; 5 5 5; 4 2 3];
area(X,Y)

image-20211022154426577

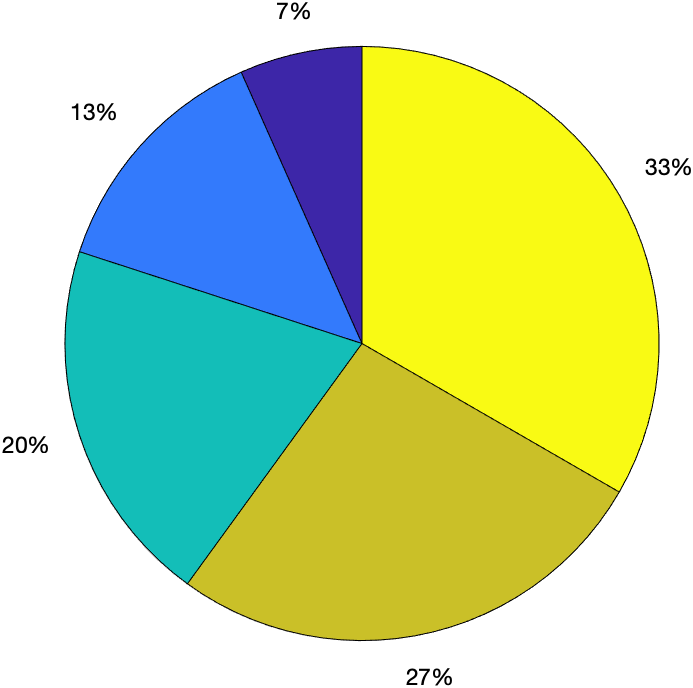
绘制饼图#

pie(x,y)

X = [1;2;3;4;5];
pie(X)

image-20211022154721546

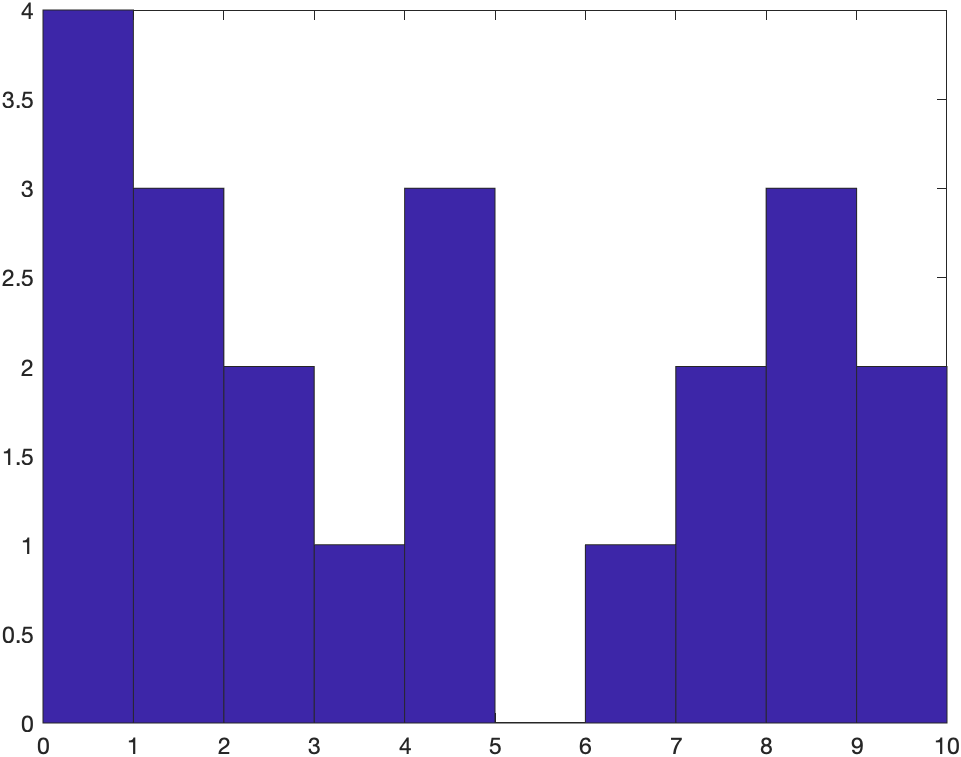
绘制直方图#

直方图统计每个区间内数据点的个数，并用柱状条表 示数据的分布情况。

直坐标#

hist()

x = [0 2 9 2 5 8 7 3 1 9 4 3 5 8 10 0 1 2 9 5 10];
hist(x)

image-20211022170928454

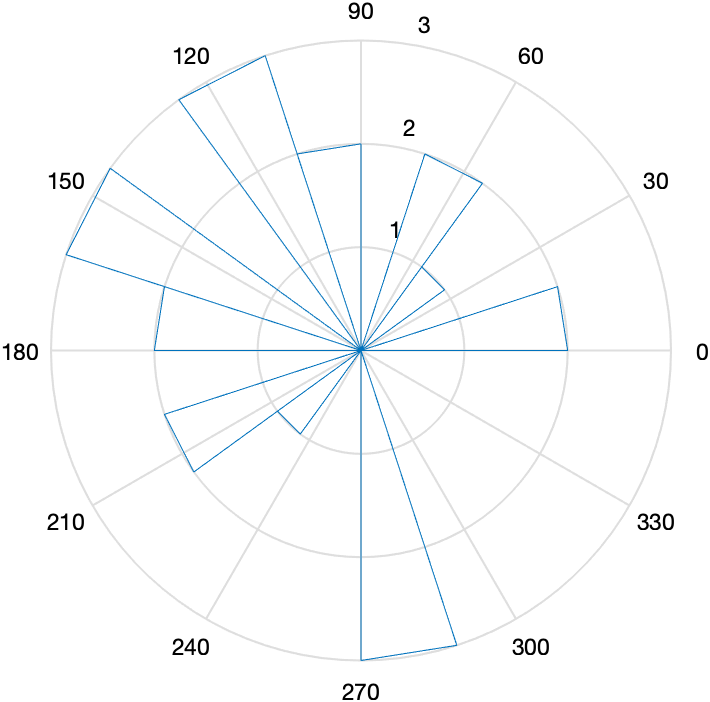
极坐标#

rose()

x = [0 2 9 2 5 8 7 3 1 9 4 3 5 8 10 0 1 2 9 5 10];
rose(x)

image-20211022171028622

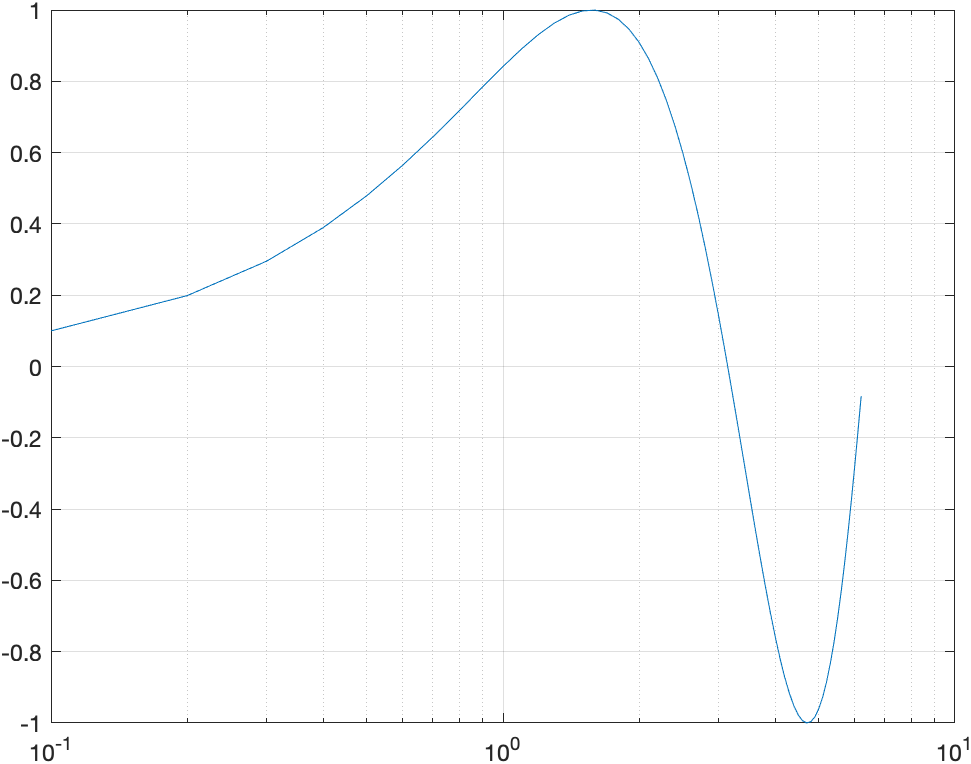
对数坐标曲线#

semilogx：半对数x坐标绘图

semilogy：半对数y坐标绘图

loglog：双对数X-Y坐标绘图

具体用法和plot相同。

x=0:0.1:2*pi; 
 y=sin(x); 
 semilogx(x,y); 
 grid on;

image-20211022175738758

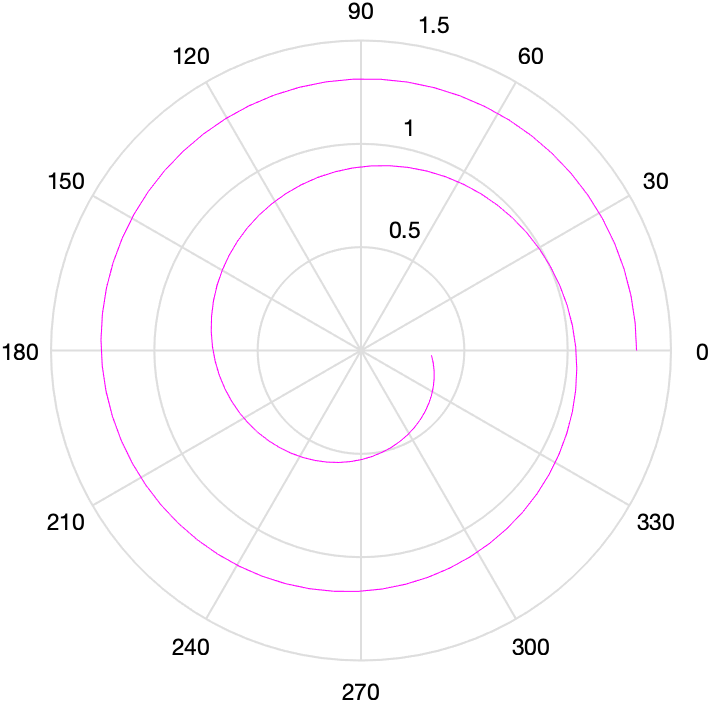
极坐标曲线#

polar(theta,rho,选项)

theta,rho分别为极角和矢径。 选项的用法和plot用法相同。

theta=0:0.1:4*pi;
rho=cos(theta/8)+1/3;
polar(theta,rho,'m-');

image-20211023000403878

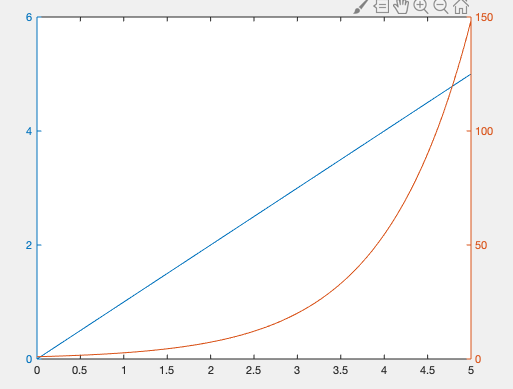
双y轴图形#

plotyy(x1,y1,x2,y2,fun);

x=0:0.01:5;
y1=x;
y2=exp(x);
plot(x,y1,x,y2);
figure
plotyy(x,y1,x,y2);

image-20211023000940800

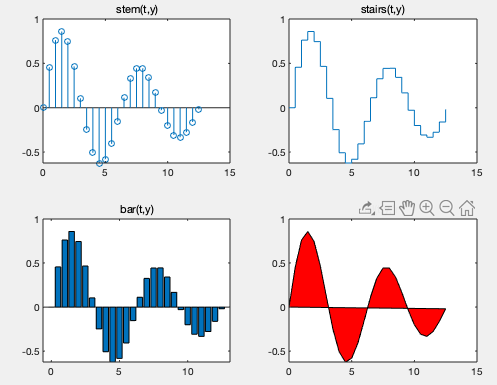
绘制二维图形的其他函数#

stem(x,y,选项)-----绘脉冲图

stairs(x,y,选项)-----绘阶梯图

fill(x1,y1,c1,x2,y2,c2,…)---用标注的颜色填 充2维多边形

t=0:0.5:4*pi;
y=exp(-0.1*t).*sin(t);
subplot (2,2,1), stem(t,y);
title('stem(t,y)')
subplot (2,2,2), stairs(t,y);
title('stairs(t,y)')
subplot (2,2,3), bar(t,y);
title('bar(t,y)')
subplot (2,2,4), fill(t,y,'r');
title(' fill(t,y,''r'')')

image-20211023001136223

三维#

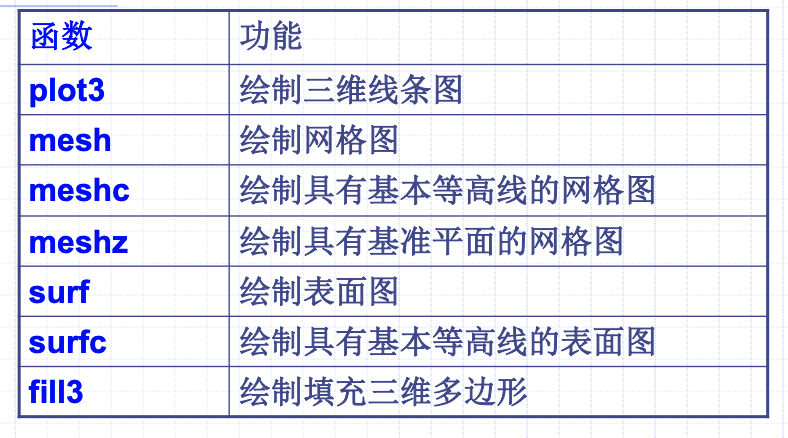
image-20211023232335195

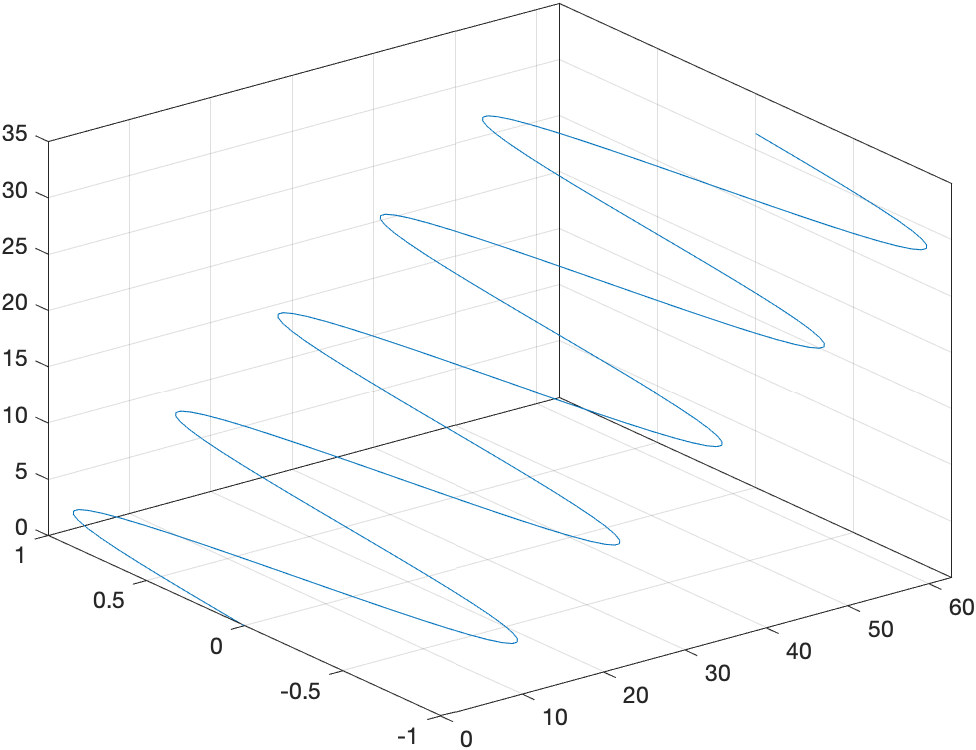
plot3() 三维曲线#

plot3(X1, Y1, Z1,LineSpec,…)

X1、Y1和Z1：三个方向上的坐标值，尺寸相同 LineSpec：对曲线的线型、颜色、线宽、点标记样 式等属性进行设置。

t = 0 : pi/20 : 10*pi; 
plot3(2*t, sin(t), t)
grid on; box on

image-20211023233037905

三维曲面#

平面网格#

[X, Y] = meshgrid(x,y)

借助surf()绘制

x、y：指定横坐标和纵坐标的一维向量；
X、Y：meshgrid函数的返回值，它们都是二维数组，X的每一行与向量x对应，Y的每一列与y对应。

x = 1:4;
y = 6:10;
[X, Y] = meshgrid(x,y)
surf(X,Y)

X =

     1     2     3     4
     1     2     3     4
     1     2     3     4
     1     2     3     4
     1     2     3     4


Y =

     6     6     6     6
     7     7     7     7
     8     8     8     8
     9     9     9     9
    10    10    10    10

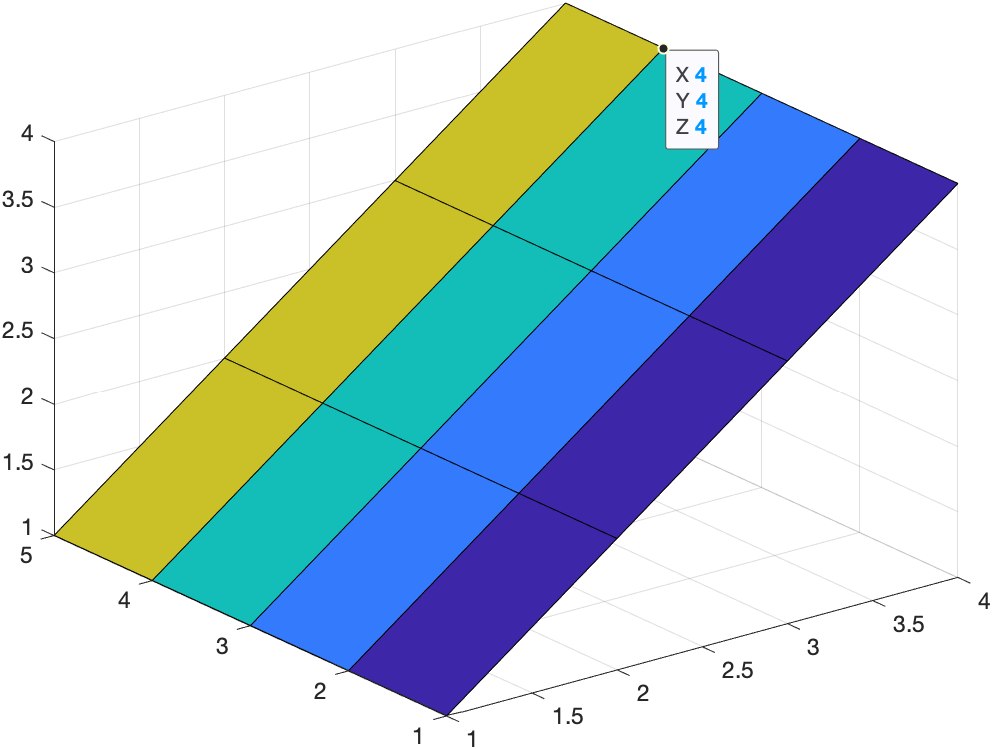
image-20211024000931302

在二维网格计算并绘制函数

x = 1:4;
y = 6:10;
[X, Y] = meshgrid(x,y)
Z = X.^2 + Y.^2 ;
surf(X,Y,Z)

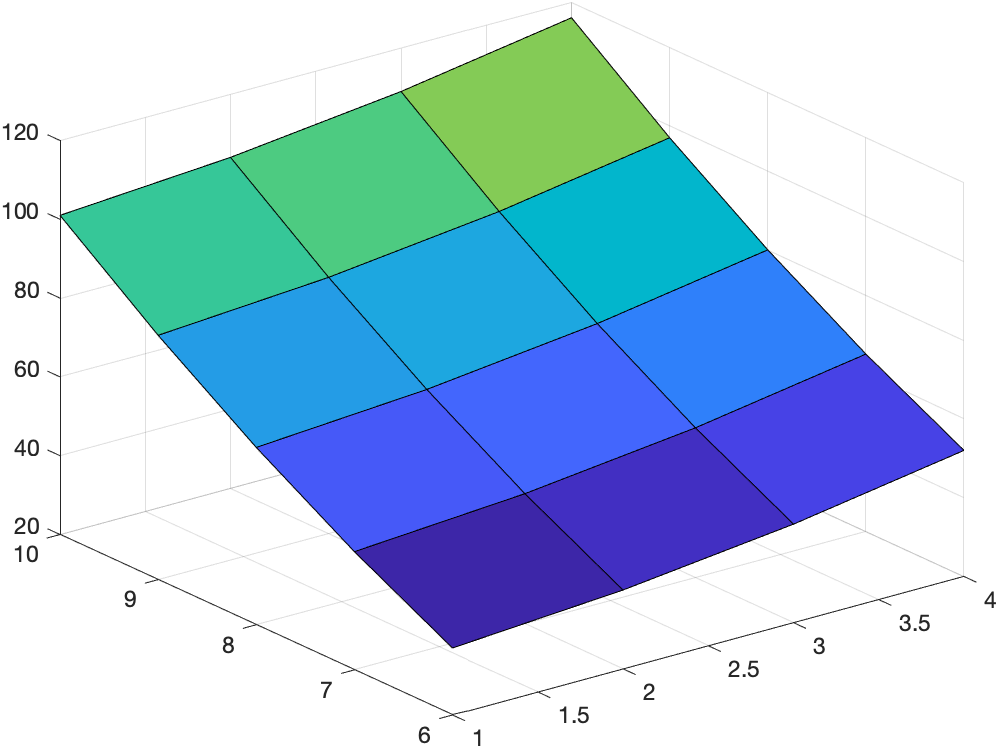
image-20211024001218898

绘制三维网眼图#

mesh函数用于三维网眼图的绘制，语法为：

 mesh(X, Y, Z)

X、Y：网格矩阵数组，一般是通过meshgrid函 数生成的二维数组；

Z：函数值数组，通过函数Z=f(X,Y)计算得到

mesh(c/z)#

meshc：在绘制网眼图的同时，在（x,y）平面上 绘制函数的等值线

meshz：在网眼图的基础上在图形的底部外侧绘 制平行与z轴的边框线（基准平面）。

x = -2:0.2:2;
y = x;
[X, Y] = meshgrid(x,y);
Z = X.^2 + Y.^2;
subplot(1,2,1); 
mesh(X,Y,Z)
title('mesh网眼图')
subplot(1,2,2); 
meshc(X,Y,Z)
title('meshc网眼图')

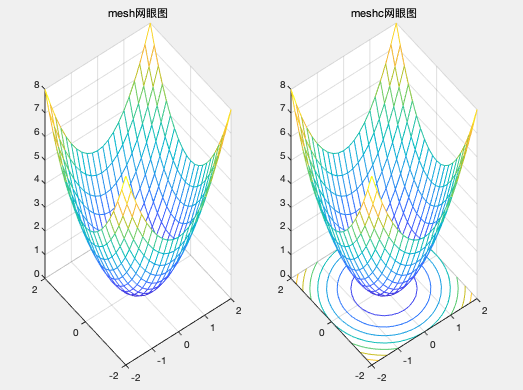
image-20211023234347152

绘制三维表面图#

surf函数用于三维表面图的绘制，语法为：

surf(X, Y, Z) surfc(X,Y,Z)

X、Y：网格矩阵数组，一般是通过meshgrid函数生成的二维数组；

Z：函数值数组，通过函数z=f(x,y)计算得到。

surf(c)#

surfc在surf的基础上绘制等值线

x = -2:0.2:2; y = x;
[X, Y] = meshgrid(x,y);
Z = -3*X + 2*Y;
subplot(1,2,1); 
surf(X,Y,Z); 
title('surf表面图')
Z2 = X.^2 + Y.^2;
subplot(1,2,2); 
surfc(X,Y,Z2); 
title('surfc表面图')

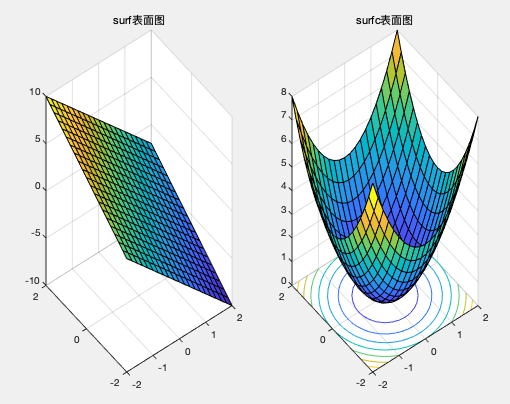
image-20211023234753912

mash与surf的比较

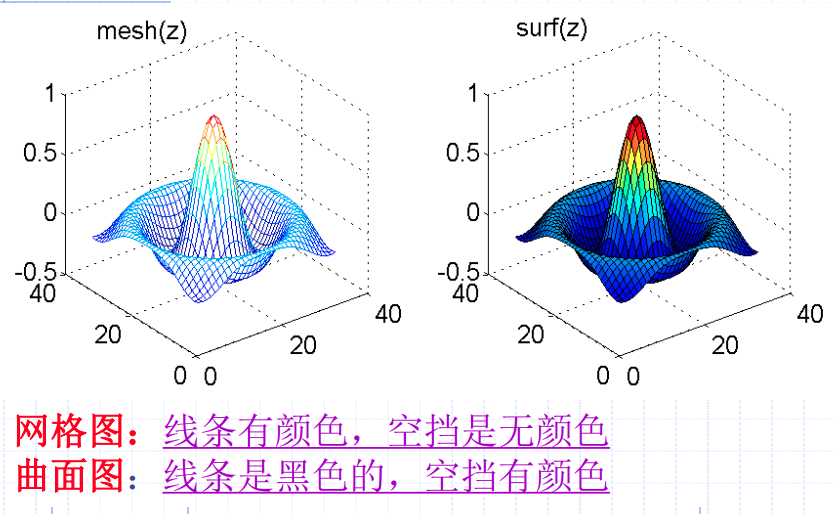
image-20211023234856661

标准三维曲面#

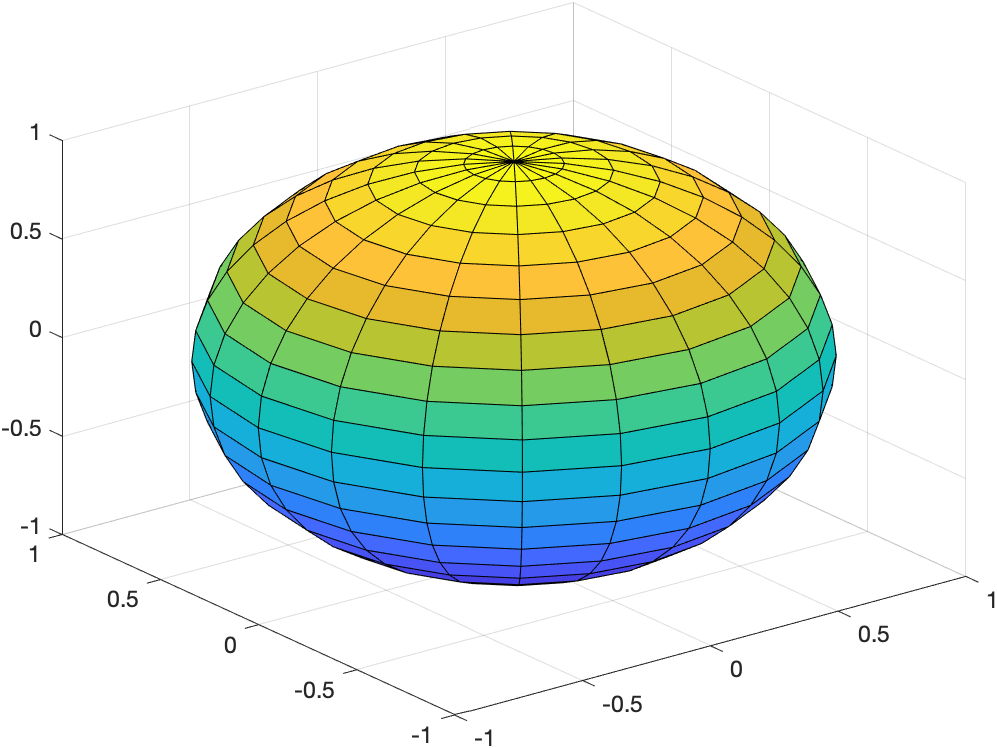
[x,y,z]=sphere(n)#

产生（n+1）×（n+1）的矩阵x，y，z，利用这三个矩阵可绘制圆心位于原点，半径为1的单位球体。

借助surf()绘制

[x,y,z] = sphere;
%绘制以原点为中心的球面。绘制两个以 (3,-2,0) 和 (0,1,-3) 为中心的球面。
figure
surf(x,y,z)

image-20211024000751094

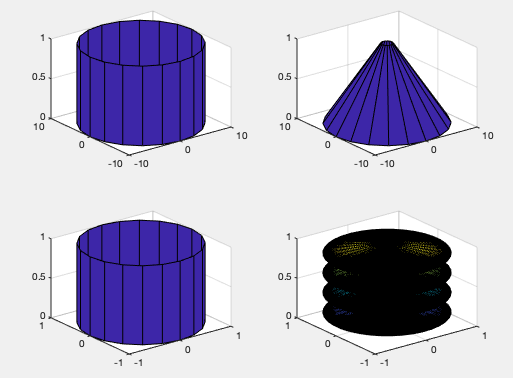
[x,y,z]= cylinder(R,n)#

R是一个向量，存放柱面各个等间隔高度上的半径

借助surf()绘制，也可以不使用，不添加返回值即可

subplot(2,2,1);[X,Y,Z]=cylinder(10);
surf(X,Y,Z)
subplot(2,2,2);cylinder([10,1]); 
subplot(2,2,3);cylinder; t=0:pi/100:4*pi; 
R=sin(t); subplot(2,2,4);cylinder(R,35);

image-20211024001539196

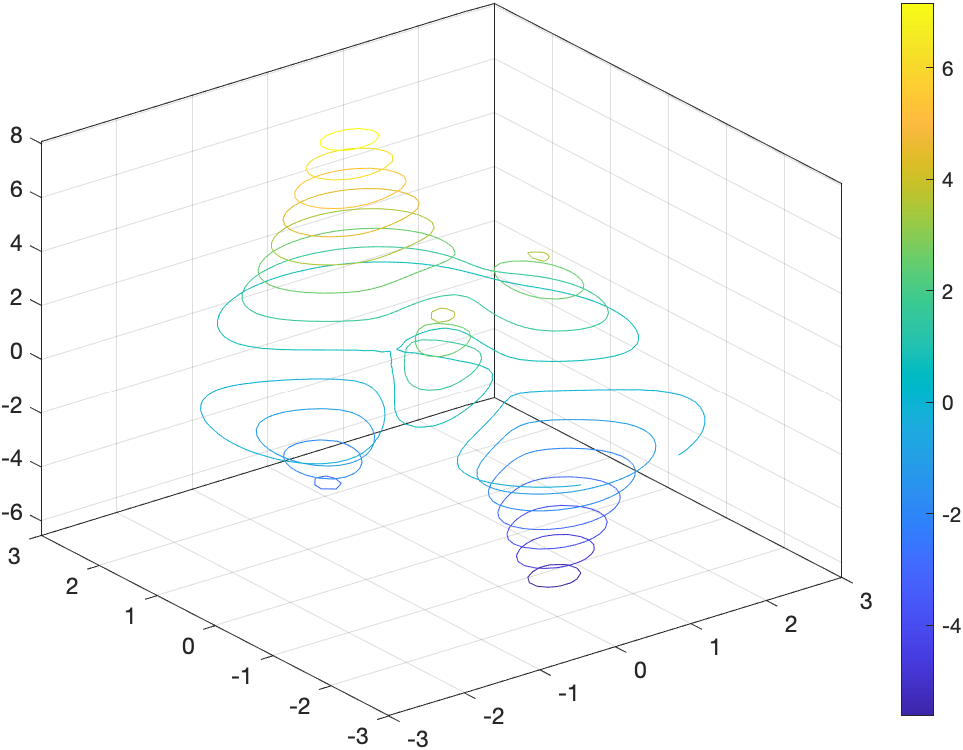
等高线图——立体#

contour3:在三维立体图中画出等高线

close all 
[x,y,z]=peaks;
contour3(x,y,z,15);
colorbar;

image-20211024001818866

三维柱状图#

bar3()

与bar()类似

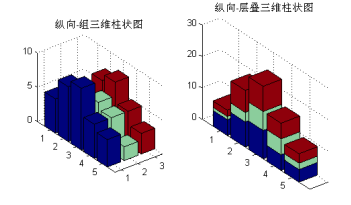
x = [1;2;3;4;5];
Y = [5 1 2;8 3 7;9 6 8;5 5 5;4 2 3];
subplot(1,2,1); 
%绘制纵向组三维柱状图
bar3(Y)
title('纵向-组柱状图')
subplot(1,2,2); 
% 绘制纵向层叠三维柱状图
bar3(x,Y,'stack') 
title('纵向层叠三维柱状图')

image-20211024002602914

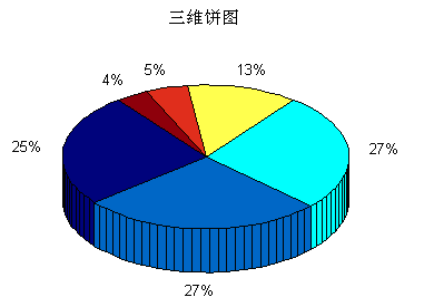
三维饼图#

pie3()

与pie()类似

X = [0.4665 0.4981 0.4874 0.2295 0.0856 0.0674]
pie3(X); title('三维饼图')

image-20211024002738667

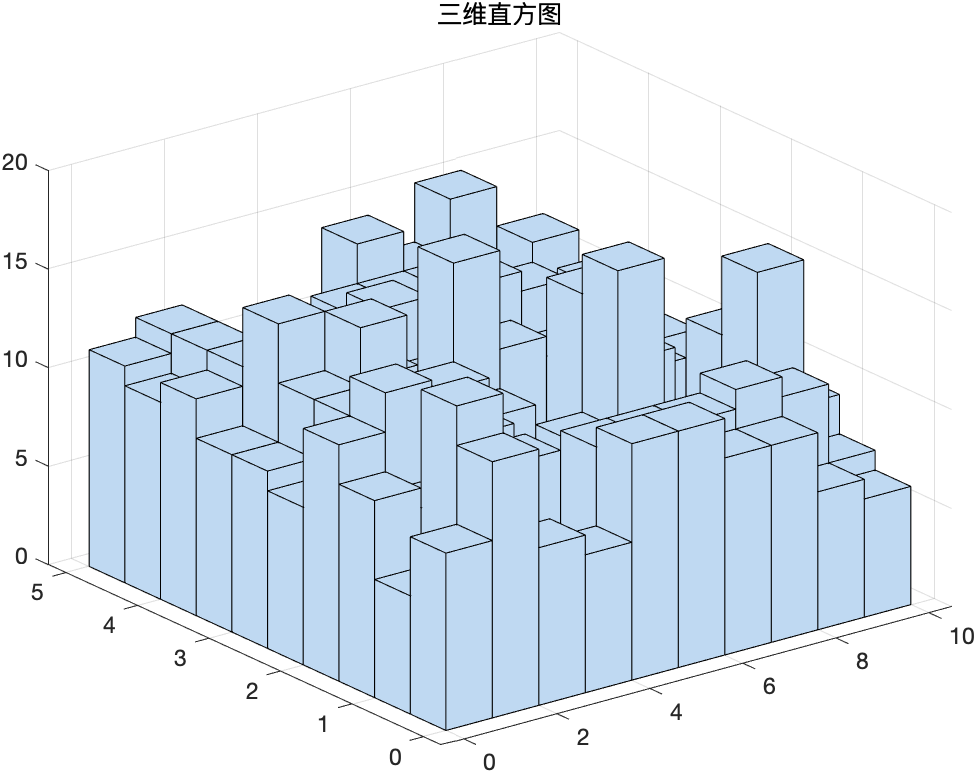
三维直方图#

hit3()

与hit()类似

X = [rand(1,1000)*10; rand(1,1000)*5]; 
X = X';
hist3(X,[10,10]); 
title('三维直方图')

image-20211024002949758

设置样式与标记属性#

plot(linespec)#

使用linespec快速设置样式，在 调用绘图函数 中有讲解

set()#

image-20211017002116142

set(H,Name,Value)

其中H为图形句柄

例：H=plot(x,y)

设置线条颜色#

image-20211016224106508
示例

p = plot(1:10);
set(p,'Color','red')

image-20211016222340399

设置线型#

image-20211016223936017

示例

p = plot(1:10);
set(p,'LineStyle','-.');

image-20211016222641810

设置线宽#

set(h, 'LineWidth', 2)% 设置线宽

设置标记符号#

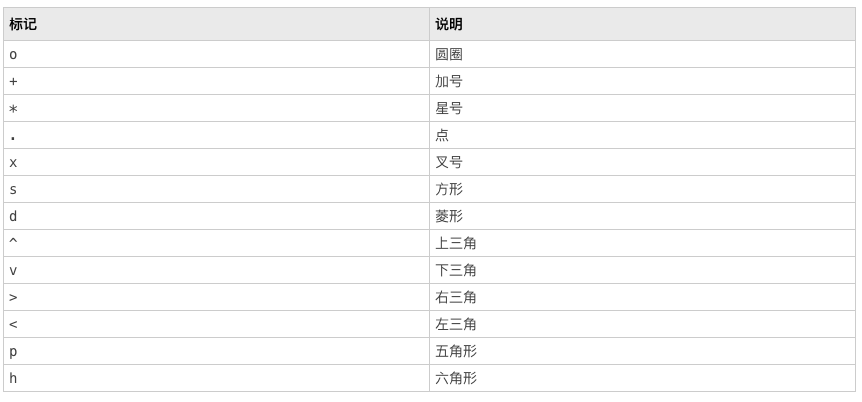
image-20211016224033885

示例

p = plot(1:10);
set(p,'Marker','*');

image-20211016222752743

设计标记点颜色#

set(h, 'MarkerEdgeColor','b'); % 设置标记点边框颜色
set(h, 'MarkerFaceColor','r'); % 设置标记点填充颜色

image-20211017002437079

设置坐标范围与网格属性#

axis()#

axis ij#

矩阵模式 i为竖轴 下至上 j为横轴 左至右

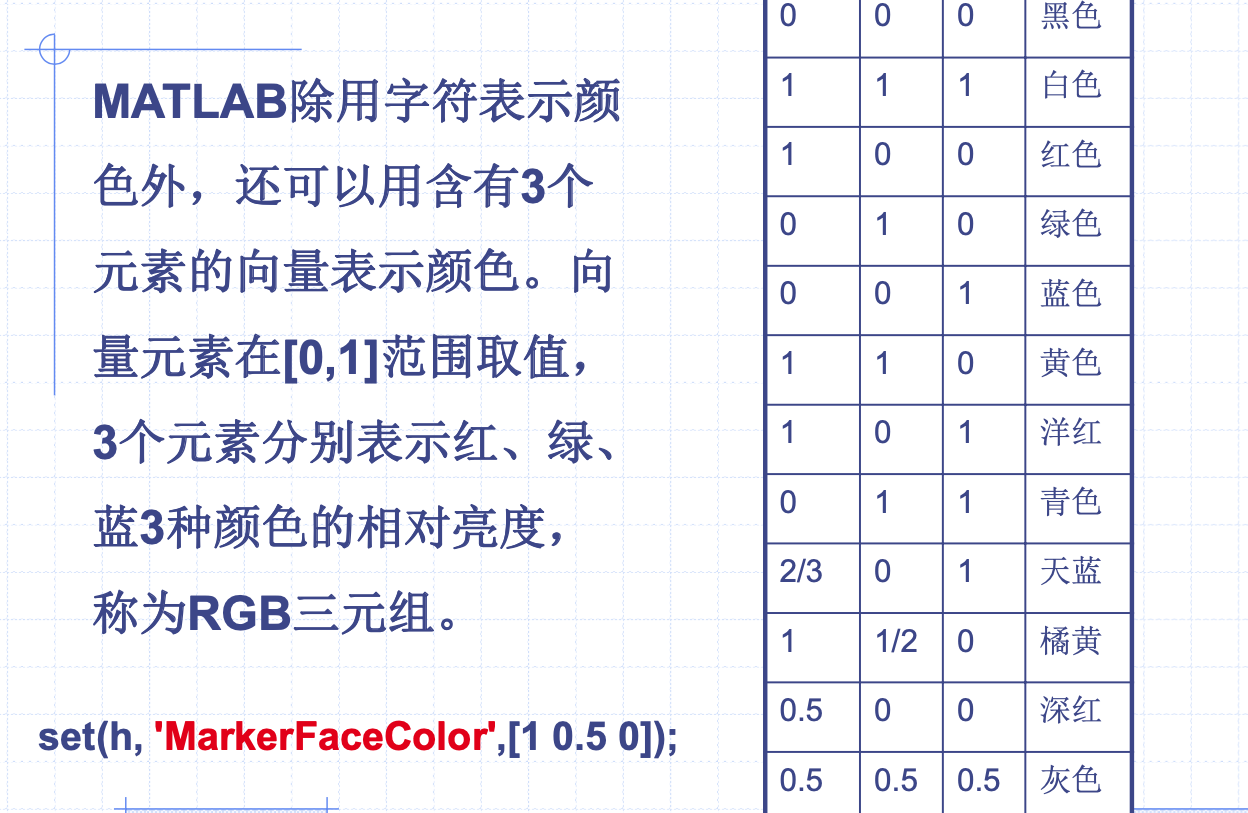
 x = 0:0.1*pi:2*pi;
y = sin(x);
plot(x,y);
% 重新设置坐标轴范围 
axis([0.2*pi 1.8*pi -1.5 1.5]) 
% 将坐标轴设置为矩阵模式 
axis ij

image-20211017003222212

axis xy#

笛卡尔模式 x为横轴 左至右 y为纵轴下至上

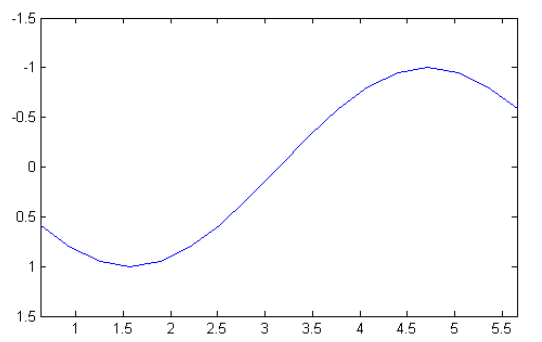
 x = 0:0.1*pi:2*pi;
y = sin(x);
plot(x,y);
% 重新设置坐标轴范围 
axis([0.2*pi 1.8*pi -1.5 1.5]) 
% 将坐标轴设置为矩阵模式 
axis xy

image-20211017003243434

设置坐标轴范围和纵横比#

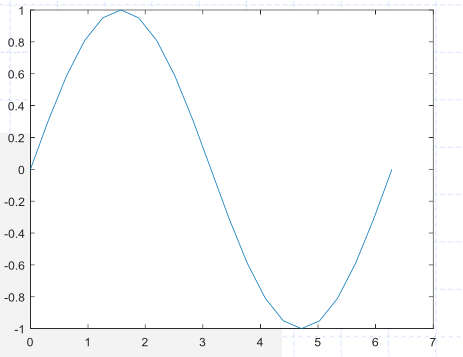
x = linspace(0,2*pi);
y = sin(x);
plot(x,y,'-o')
axis([0 2*pi -1.5 1.5])

前两组设置横轴范围，后两组设置纵轴范围

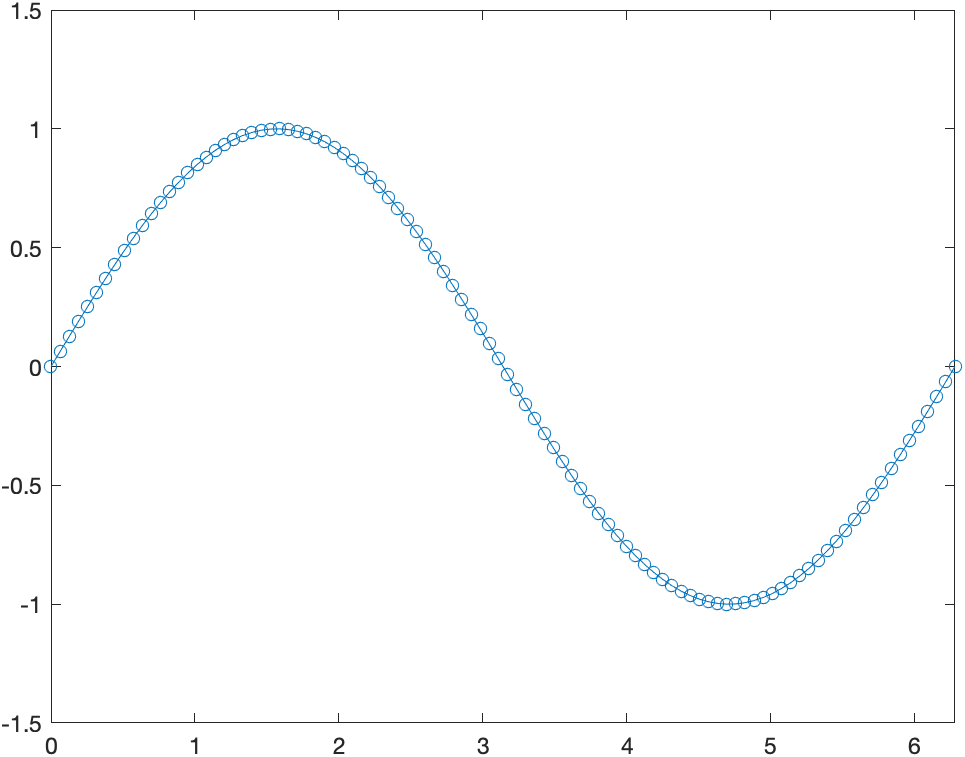
image-20211016224805771

半自动设置#

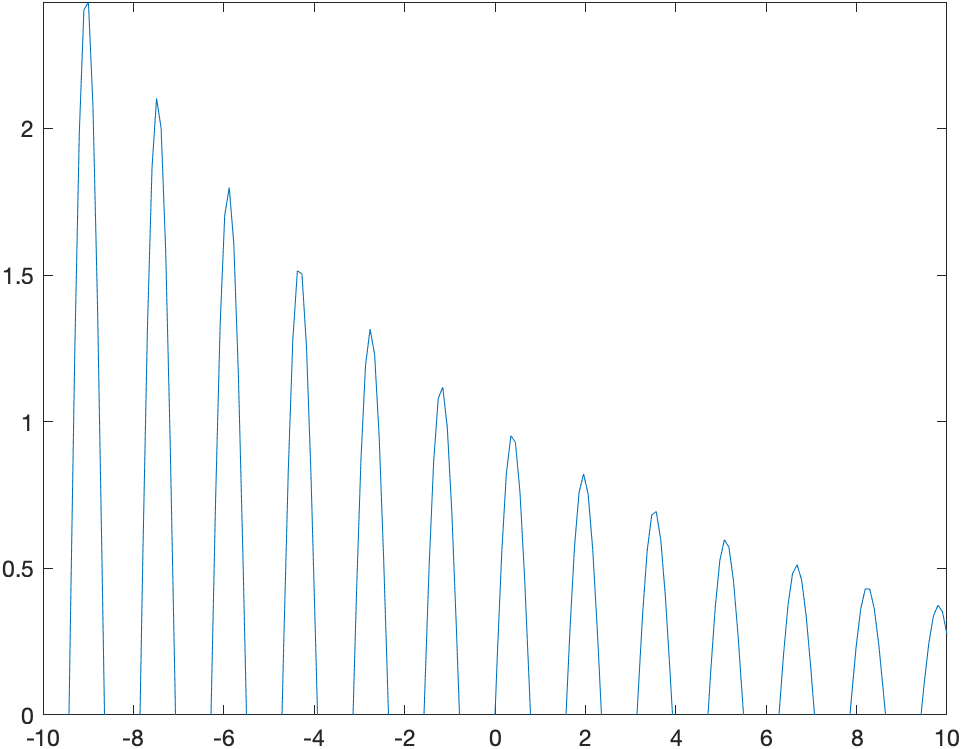
自动设置纵轴最大值

x = linspace(-10,10,200);
y = sin(4*x)./exp(.1*x);
plot(x,y)
axis([-10 10 0 inf])

image-20211016225018019

自动设置#

axis auto

冻结范围#

axis manual

设置为数据范围#

axis tight

显示或隐藏坐标轴（常用在3d）#

axis on
axis off

grid#

显示或隐藏坐标区网格线

grid on
grid off

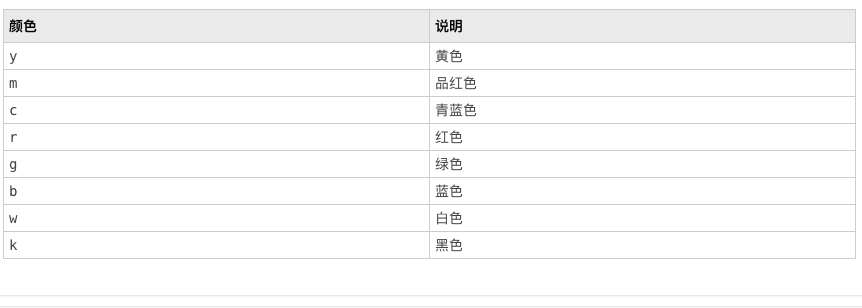
设置色表#

colormap < name >

image-20211024002137848

设置光照效果#

shading flat：将图形对象（线条、表面区域 等）显示为单色；

shading faceted：将图形对象显示为单色，将 线条对象显示为黑色；（默认）

shading interp：将图形对象显示为颜色过渡 模式。

设置视角#

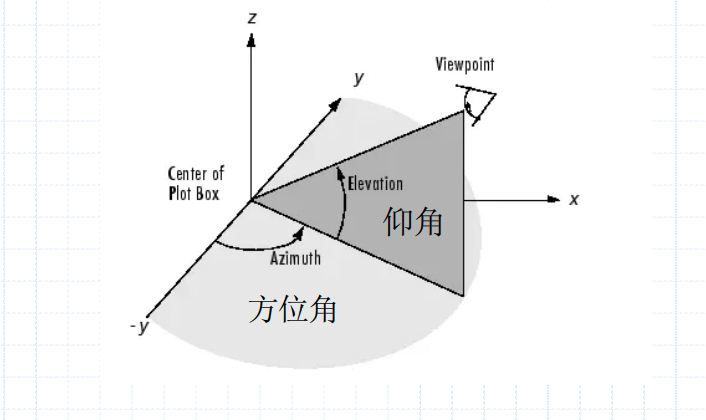
image-20211024001924106

view(az, el) view([az, el]）

[az, el] = view az：视角的方位角 el：视角的仰角。

[az, el] = view返回当期 视角的方位角和仰角

给图形添加标注#

title()设置标题#

title ('the first figure ');

xlabel()横坐标标签#

xlabel ('横坐标');

ylable()纵坐标标签#

ylabel ('纵坐标');

legend()设置图例#

legend('tan(sin(x)) - sin(tan(x))');

image-20211017002818816

colorbar设置颜色条#

image-20211022151351754

annotation添加文本、线条、箭头、图框#

image-20211022151405852

导出或保存图形#

print()#

print(gcf,'my_first_figure.jpg','-djpeg')
matlab图像绘制
https://kozakemi.top/posts/matlab图像绘制/
作者
Kozakemi
发布于
2021-10-18
许可协议
CC BY-NC-SA 4.0
Keil uVision5 C51安装+烧录工具
数据结构实验
© 2024 Kozakemi. All Rights Reserved. / RSS / Sitemap
Powered by Astro & Fuwari